Writing a Custom Bounce Function
Easing functions are becoming particularly ubiquitous in user interfaces. They add a lot of personality to your UI, creating a playful, unobtrustive experience to layer on top of your UI's functionality. Perhaps at some point you'll want to write a custom easing function. These functions tend to be pretty simple polynomials exponentials, etc. But a bounce function is rather unique in that it's a collection of piecewise functions that all need to line up correctly to simulate the decay of a rigid, plastic collision over time.
A bounce ease functions is just a group of n discontinuous functions along the domain [0, 1], where n is the number of bounces you want. So we will design a series of parabolic functions so that their y=1 intercepts all touch each other, and manipulate their maxima/apexes to imitate a nicely decaying bounce.
To do this you need to know how to shift a function, how to flip a function, and how to scale/stretch a function. Read over this webpage for an overview.
We can write out polynomial functions in factored form in order to easily assign what their roots (y=0 intercepts) will be. Let's work with quadratics to keep things simple (Using qaurtic, octic parabolas would change the smoothness of your curves). So a function will be of the form:
f(x) = scalar * (x-root1)(x-root2) + constant
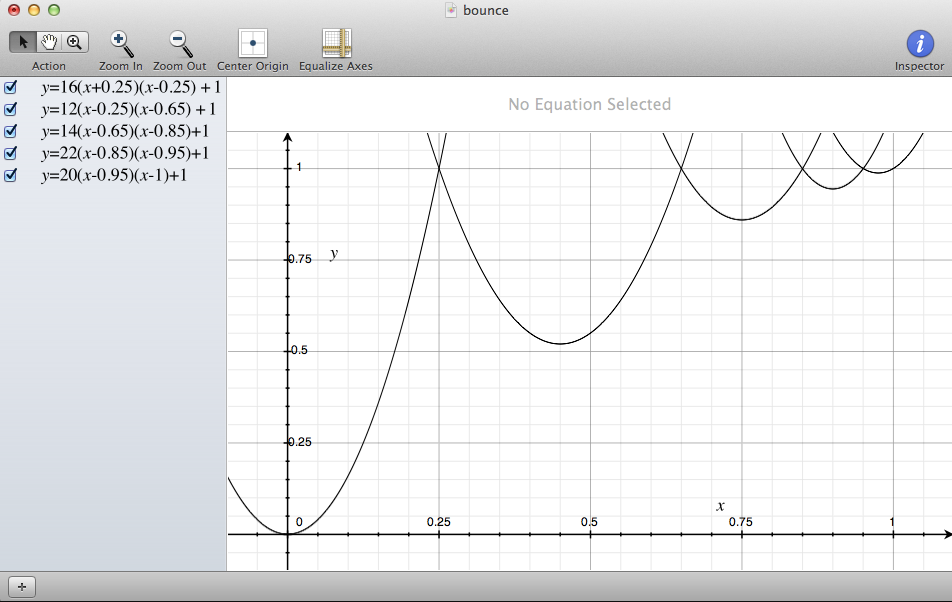
Since we want the bounce to occur at y=1 rather than y=0, we add a constant value of 1 to all our functions. In order to make our bounce functions have their y=1 intercepts line up, you have to feed the right-most y=1 intercept of one function into the next.
Let's say we want four bounces. Our equations would look like:
f1(x)=a1(x+r0)(x-r1)+1 // Note: make r0 = r1 to center function's maxima at x=0 f2(x)=a2(x-r1)(x-r2)+1 f3(x)=a3(x-r2)(x-r3)+1 f4(x)=a4(x-r3)(x-1) +1 // r4 = 1 because easing functions typically end at x=1
Once you have set up this system of equations, tune the locations of your y=1 intercepts (r0 through r3), and your scalars (a1 through a4) to give the desired spacing and amplitudes of your bounces. Here is an example I made in the Apple utility Grapher:
So now the hard part is over, we have our piece-wise functions. Here is some pseudo code tying them all together. Basically we have to pick the proper function based on where we lie on the [0,1] domain:
bounce(x): x = clamp(x,0,1) if x >= 0 and x < r1 then return f1(x) elseif x >= r2 and x < r3 then return f2(x) ... else return fn(x) end
Where f1, f2, ..., fn are your functions (but multiply things out as much as possible, consolidate constants, etc) and r1, r2, ..., rn are the y=1 intercepts of your functions.
Basics of Manipulating Functions
Easings.net, amazing resource for visualizing different easing functions